Reversible Computing: The Next Generation of Software Construction Theory

Contact me

As we all know, the cornerstones of computer science are two basic theories: Turing machine theory proposed by Turing in 1936 and Lambda calculus theory published by Church in the early same year. These two theories laid the conceptual foundation of the so-called Universal Computation, describing two technical routes with the same computing power (Turing complete), but with different forms. If we regard these two theories as the two extremes of the world origin shown by God, is there a more moderate and flexible way to reach the other side of general computing?

Since 1936, software, as the core application of computer science, has been in the process of continuous conceptual change, and various programming languages/system architectures/design patterns/methodologies have emerged in an endless stream, but the basic principles of software construction are still within the scope of the two basic theories. If a new theory of software construction is defined, what is essentially unique about the new concepts it introduces? What thorny problems can be solved?

In this paper, the author proposes that a new core concept-reversibility can be naturally introduced on the basis of Turing machine and lambda calculus, thus forming a new software construction theory, Reversible Computation. Reversible computing provides a higher level of abstraction that is different from the current mainstream methods in the industry, which can greatly reduce the inherent complexity of software and remove the theoretical obstacles for coarse-grained software reuse.

The idea of reversible computation comes not from computer science itself, but from theoretical physics. It regards software as an abstract entity in the process of continuous evolution, which is described by different operation rules at different levels of complexity. It focuses on how the small differences generated in the process of evolution propagate orderly and interact in the system.

The first section of this paper will introduce the basic principles and core formulas of reversible computing theory. The second section will analyze the differences and connections between reversible computing theory and traditional software construction theories such as component and model-driven, and introduce the application of reversible computing theory in the field of software reuse. The third section will deconstruct innovative technology practices such as Docker and React from the perspective of reversible computation.

One. Fundamentals of reversible computation

Reversible computation can be seen as a necessary consequence of the application of Turing computation and lambda calculus to model the world in a real world with limited information, which can be understood by the following simple physical picture. First, a Turing machine is a structurally fixed machine that has an enumerable finite set of States, can only perform a limited number of operations, but can read and save data from an infinite length of paper tape. For example, the computer we use daily, its hardware function has been determined when it leaves the factory, but by installing different software and importing different data files, it can automatically produce any complex target output. The computing process of a Turing machine can be formally written as

\[TargetOutput = FixedMachine（InfiniteInput）\]

Contrary to Turing machine, the core concept of lambda calculus is function. A function is a small computing machine. The composition of function is still a function, that is to say, more complex machines can be produced by recursive combination of machines and machines. The computational power of lambda calculus is equivalent to that of Turing machine, which means that if we are allowed to create more complex machines, even if we input a constant 0, we can get arbitrarily complex target output. The computational procedure of lambda calculus can be formally written as

\[TargetOutput = InfiniteComposableMachine（FixedInput）\]

It can be seen that the above two calculation processes can be expressed in the abstract form of Y = F (X). If we understand Y = F (X) as a modeling process, that is, we try to understand the structure of the input and the mapping relationship between the input and the output, and reconstruct the output in the most economical way, we will find that Turing machines and lambda calculus assume conditions that cannot be satisfied in the real world. In the real physical world, human cognition is always limited, and all quantities need to distinguish between the known part and the unknown part, so we need to decompose as follows:

\[\begin{aligned} Y &= F(X) \\ &= (F_0 + F_1) (X_0+X_1)\\ &= F_0(X_0) + \Delta \end{aligned}\]

Rearranging the notation, we get a much more widely applicable computational model.

\[Y = F(X) \oplus \Delta\]

In addition to the functional operation F (X), there is a new structural operator ⊕, which represents the composition operation between two elements, not the addition in the ordinary numerical sense, and leads to a new concept: difference △. The peculiarity of △ is that it must contain some kind of negative element, and the result of the combination of F (X) and △ is not necessarily an “increase” in output, but a “decrease”. In physics, the necessity of the existence of delta and the fact that delta contains an inverse element are self-evident, because the modeling of physics must take into account two basic facts:

  1. The world is “unpredictable”, and noise is always there.

  2. The complexity of the model should match the intrinsic complexity of the problem, which captures the stable trends and laws in the kernel of the problem.

For example, for the following data

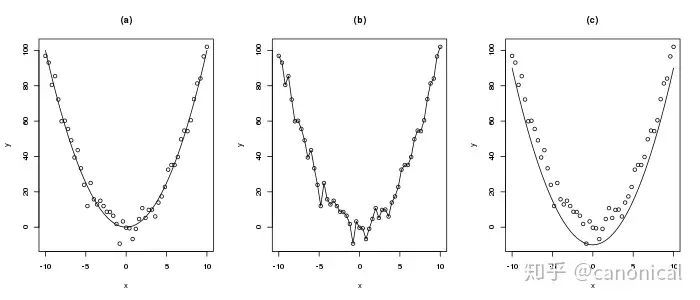
The model we have built can only be a simple curve similar to that in Figure (a). The model in Figure (B) tries to accurately fit each data point, which is mathematically called overfitting. It is difficult to describe new data. In Figure (C), the limit difference can only be positive, which will greatly limit the accuracy of the model.

The above is a heuristic description of the abstract computing pattern Y = F (X) △. Next, we will introduce a specific technical implementation scheme for implementing this computing pattern in the field of software construction, which is named reversible computing by the author. The so-called reversible calculation refers to a technical route of systematically applying the following formula to guide software construction

\[App = Delta\ \text {x-extends}\ Generator \langle DSL \rangle\]

DSL is a high-density representation of critical domain information, which directly directs the Generator to generate code, similar to Turing computing, which drives the machine to execute built-in instructions through input data. If the Generator is regarded as the substitution generation of text symbols, its execution and composition rules are a complete copy of lambda calculus. In a sense, differential merging is a very novel operation, because it requires us to have a meticulous and omnipotent change collection ability, which can separate and merge the small quantities of the same order scattered all over the system, so that the differential has the meaning and value of independent existence. At the same time, the concepts of inverse element and inverse operation must be clearly established in the system, in which the difference can be expressed as a mixture of “existence” and “non-existence”.

The existing software infrastructure cannot effectively implement reversible computing without a thorough transformation. Just as the Turing machine model gave birth to C language and Lambda calculus gave birth to Lisp language, in order to effectively support reversible computation, the author proposes a new programming language X language, which has built-in key features such as difference definition, generation, merging and splitting, and can quickly establish domain models and realize reversible computation on the basis of domain models. In order to implement reversible computation, we must establish the concept of difference. The change produces a differential, which can be positive or negative, and should meet the following three requirements

In the third section, the author will take Docker as an example to illustrate the importance of these three requirements.

The core of reversible computing is “reversible”, which is closely related to the concept of entropy in physics. Its importance is far beyond the program construction itself. In the article “The methodological origin of reversible computing”, the author will elaborate on it in more detail.

Just as the emergence of complex numbers expands the solution space of algebraic equations, reversible computing adds the key technical means of “reversible difference merging” to the existing software construction technology system, thus greatly expanding the feasible scope of software reuse and making it possible to reuse coarse-grained software at the system level. At the same time, under the new perspective, many model abstraction problems that were difficult to solve before can find simpler solutions, thus greatly reducing the inherent complexity of software construction. In the second section, the author will elaborate on this.

Although software development is known as knowledge-intensive work, up to now, the daily life of many front-line programmers still contains a large number of mechanized manual operations of code copying/pasting/modification, and in the theory of reversible computing, the modification of code structure is abstracted as an automatically-executable rule of difference merging, so through reversible computing. We can create the basic conditions for the automated production of software itself. On the basis of reversible computing theory, a new software industrialization production mode NOP (Nop is nOt Programming) is proposed, which produces software in batches in a non-programming way. NOP is not programming, but it does not mean no programming. It emphasizes the separation of the logic that business people can intuitively understand from the logic at the level of pure technical implementation, using appropriate languages and tools to design, and then seamlessly bonding them together. The author will introduce NOP in detail in another article. Reversible computing and reversible computer have the same source of physics thought. Although the specific technical connotation is not consistent, their goals are unified. Just as cloud computing tries to realize the cloud of computing, reversible computing and reversible computers try to realize the reversibility of computing.

Two. Reversible Computing: Inheritance and Development of Traditional Theory

(I) Component

The birth of software originated from the by-product of mathematicians’ research on Hilbert’s tenth problem. The main purpose of early software was also mathematical physics calculation. At that time, the concepts in software were undoubtedly abstract and mathematical. With the popularization of software, more and more research and development of application software have given birth to object-oriented and component-based methodologies, which try to weaken abstract thinking and turn to human common sense, draw knowledge from people’s daily experience, map concepts that people can intuitively perceive in the business field to objects in the software, and imitate the production process of the material world. The construction of the final software product is achieved by piecing and assembling step by step. Concepts familiar to the software development world, such as frameworks, components, design patterns, and architectural views, all come directly from the production experience of the construction industry. Component theory inherits the essence of object-oriented thinking, creates a huge third-party component market with the concept of reusable prefabricated components, and achieves unprecedented technical and commercial success. Even today, it is still the most mainstream guiding ideology of software development. However, there is an essential defect in the component theory, which prevents it from pushing its success to a new height. We know that the so-called reuse is the reuse of existing products. In order to achieve component reuse, we need to find the common part of the two software, separate it and organize it into a standard form according to the component specification. However, the granularity of the common part of A and B is smaller than that of both A and B, and the common part of a large number of software is much smaller than the granularity of any one of them. This limitation directly leads to the fact that the larger the granularity of software functional modules, the more difficult it is to be directly reused, and there is a theoretical limit to component reuse. Component assembly can reuse 60% -70% of the workload, but few people can exceed 80%, let alone achieve system-level overall reuse of more than 90%. In order to overcome the limitations of component theory, we need to re-recognize the abstract nature of software. Software is an information product that exists in an abstract logical world, and information is not material. The structure and production laws of the abstract world are essentially different from those of the material world. The production of material products always has a cost, while the marginal cost of copying software can be zero. To remove a table from a room, you have to go through a door or window in the physical world, but in the abstract information space, you just need to change the coordinates of the table from X to -x. The operational relationship between abstract elements is not limited by many physical constraints, so the most effective mode of production in the information space is not to assemble, but to master and formulate operational rules. If we re-interpret object-oriented and component technology from a mathematical point of view, we will find that reversible computing can be regarded as a natural extension of component theory. Object-oriented: Inequality A > B Component: Addition A = B + C Reversible Computation: Difference Y = X + △ Y One of the core concepts in object-oriented is inheritance: derived classes inherit from the base class and automatically have all the functions of the base class. For example, tiger is a derivative of animal. In mathematics, we can say that the concept of tiger (A) contains more content than the concept of animal (B), tiger > animal (that is, A > B). According to this, we can know that the tiger naturally satisfies the proposition satisfied by the concept of animal, for example, if the animal can run, the tiger must also run (P (B)-> P (A)). Everywhere the concept of an animal is used in the program, it can be replaced by a tiger (the Liscov substitution principle). In this way, automatic reasoning is introduced into the field of software through inheritance, which corresponds to inequality in mathematics, that is, a partial order. The theoretical dilemma of object orientation lies in the limited expressive power of inequalities. For the inequality A > B, we know that A is more than B, but we have no way to express exactly what is more. In the case of A > B, D > E, even if the extra part is the same, we can’t reuse this part of the content. Component technology explicitly States that “composition is superior to inheritance”, which is equivalent to the introduction of addition

\[A = B + C \\ D = E + C\]

In this way, component C can be abstracted for reuse.

Following the above direction, we can easily determine that the next step is to introduce “subtraction”, so that A = B + C can be regarded as a real equation, which can be solved by shifting the left and right terms of the equation.

\[B = A - C = A + (-C)\]

The “negative component” introduced by subtraction is a new concept, which opens a new door for software reuse. Assuming that we have constructed the system X = D + E + F, we now need to construct Y = D + E + G. If you follow the solution of components, you need to disassemble X into several components, then replace component F with G and reassemble it. If we follow the technical route of reversible computation, by introducing the inverse element -F, we immediately get

\[Y = X - F + G = X + (-F + G) = X + \Delta Y\]

Without disassembling X, system X can be transformed into system Y by directly appending a difference △ Y. The reuse condition of components is “the same can be reused”, but in the case of the existence of inverse elements, the complete system X with the maximum granularity can be reused directly without any change, the scope of software reuse is expanded to “relevant can be reused”, and the granularity of software reuse is no longer limited. The relationship between components has also undergone profound changes, which is no longer a monotonous composition relationship, but a more diverse transformation relationship. The physical image of Y = X + △ Y has a very realistic significance for the development of complex software products. X can be the basic version or the main version of the software product we developed. When it is deployed and implemented at different customers, a large number of customization requirements are isolated into independent delta △ Y. These customized delta descriptions are stored separately and merged with the main version code through compilation technology. The architecture design and code implementation of the main version only need to consider the stable core requirements in the business area, and will not be impacted by the accidental requirements of specific customers, thus effectively avoiding the corruption of the architecture. The development of the main version and the implementation of multiple projects can be carried out in parallel. Different implementation versions correspond to different △ Y and do not affect each other. At the same time, the code of the main version is independent of all customized codes and can be upgraded as a whole at any time.

(II) Model Driven Architecture

Model Driven Architecture (MDA) is a software architecture design and development method proposed by Object Management Group (OMG) in 2001, which is regarded as a milestone in the transformation of software development mode from code-centric to model-centric. At present, the theoretical basis of most so-called software development platforms is related to MDA.

MDA attempts to raise the level of abstraction in software development, using a modeling language (such as Executable UML) directly as the programming language, and then translating the high-level model into the underlying executable code by using compiler-like techniques. In MDA, application architecture and system architecture are clearly distinguished, and they are described by PIM (Platform Independent Model) and PSM (Platform Specific Model) respectively. PIM reflects the function model of the application system, which is independent of the specific implementation technology and running framework, while PSM focuses on using specific technologies (such as J2EE or dotNet) to implement the functions described by PIM and provide a running environment for PIM.

The ideal scenario for using MDA is that developers use visual tools to design PIM, then select the target running platform, and the tools automatically execute the mapping rules for specific platforms and implementation languages, transform PIM into corresponding PSM, and finally generate executable application code. The MDA-based program construction can be formulated as follows

\[App = Transformer(PIM)\]

MDA’s vision is to eventually eliminate traditional programming languages in the same way that C replaced assembly. However, after so many years of development, it has not been able to show an overwhelming competitive advantage over traditional programming in a wide range of applications.

In fact, the current development tools based on MDA are always difficult to hide their inherent inadaptability in the face of changing business areas. According to the analysis in the first section of this paper, we know that the modeling must consider the difference. In the construction formula of MDA, the App on the left side represents various unknown requirements, while the Transformer and PIM designers on the right side are actually mainly provided by development tool vendors. Such an equation as unknown = known cannot maintain a balance for a long time. At present, the main approach of tool vendors is to provide a large and complete set of models, trying to predict all possible business scenarios of users in advance. However, we know that “there is no free lunch in the world”, the value of the model is to reflect the essential constraints in the business field, and no model is optimal in all scenarios. Predicting demand can lead to a paradox: if the model has too few built-in assumptions, it cannot automatically generate a large amount of useful work based on a small amount of information input by the user, nor can it prevent the user from misoperation, and the value of the model is not obvious. On the contrary, if the model has many assumptions, it will be solidified to a specific business scenario, and it is difficult to adapt to new situations.

When we open the designer of an MDA tool, we often feel that most of the options are not needed, and we don’t know what they are used for, but we can’t find the options we need everywhere. Reversible computing extends MDA in two ways:

  1. Both Generators and DSLs in reversible computing encourage users to expand and adjust, which is similar to language-oriented programming.
  2. There is an additional opportunity for delta customization to make precise local corrections to the overall generation result.

In the NOP production pattern proposed by the author, a new key component must be included: the designer of the designer. Ordinary programmers can use the designer of the designer to quickly design and develop their own domain specific language (DSL) and its visual designer, and at the same time, they can customize and adjust any designer in the system through the designer of the designer, and freely add or delete elements.

Aspect oriented programming (Aspect Oriented Programming)

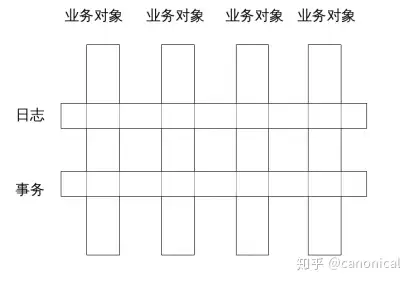
Aspect-Oriented Programming (AOP) is a programming paradigm that complements Object-Oriented Programming (OOP) by encapsulating so-called cross-cutting concerns that span multiple objects. For example, a requirement specification might specify that all business operations be logged and that all database modifications be transacted. According to the traditional object-oriented implementation, a sentence in the requirement will lead to a sudden expansion of redundant code in many object classes, and through AOP, these common “decorative” operations can be stripped into independent aspect descriptions. This is the so-called orthogonality of the longitudinal and transverse decompositions.

AOP is essentially a combination of two capabilities:

  1. Locate the target pointcut in the program structure space
  2. The local program structure is modified to Weave the extended logic (Advice) to the specified location.

Localization relies on the existence of a well-defined global structure coordinate system (how can one locate without coordinates?) While the modification relies on the existence of a well defined local program semantic structure. The limitation of the current mainstream AOP technology is that they are all expressed in the object-oriented context, and the domain structure is not always consistent with the object implementation structure, or it is not sufficient to express the domain semantics with the coordinates of the object system. For example, applicant and approver are different concepts that need to be clearly distinguished in the domain model, but they may correspond to the same Person class at the object level. In many cases, AOP cannot directly convert the domain description into pointcut definition and Advice implementation. This limitation is reflected at the application level, and as a result, we don’t find a place for AOP except for a few “classic” applications such as logging, transactions, lazy loading, caching, and so on, which are not related to a specific business domain.

Reversible computation requires localization and structural modification capabilities similar to AOP, but it defines these capabilities in the domain model space, thus greatly expanding the scope of AOP. In particular, the structured difference △ generated by the self-evolution of the domain model in reversible computing can be expressed in a form similar to the AOP aspect. We know that components can identify recurring “identities” in programs, and that reversible computation can capture “similarities” in program structure. Similarities are rare and require keen discrimination, but in any system, there is a similarity that is readily available, that is, the similarity between the system and its own historical snapshots in the process of dynamic evolution. This similarity has no special technical expression form in the previous technical system.

Through vertical and horizontal decomposition, the concept network we have established exists in a design plane. When the design plane evolves along the time axis, it will naturally produce a “three-dimensional” mapping relationship: the design plane at the next moment can be regarded as adding a difference mapping (customization) from the plane at the previous moment, and the difference is defined at each point of the plane. This picture is similar to the notion of Functor in Category theory, where the conflation of differences in reversible computation plays the role of a Functor map. Therefore, reversible computing is equivalent to expanding the original design space and finding a specific technical form of expression for the concept of evolution.

(IV) Software Product Line

The theory of software product line originates from an insight that in a business field, few software systems are completely unique, and there are similarities in form and function among a large number of software products, which can be attributed to a product family. All products in a product family (existing and not yet existing) are studied, developed and evolved as a whole. Through scientific methods to extract their commonalities, combined with effective variability management, it is possible to achieve large-scale, systematic software reuse, and then achieve the industrial production of software products.

Software product line engineering (SPle) uses a two-stage lifecycle model to distinguish between domain engineering and application engineering. The so-called domain engineering refers to the process of analyzing the commonness of software products in the business domain, establishing domain models and common software product line architectures, and forming reusable core assets, that is, development for reuse. The essence of application engineering is to use reuse to develop (development with reuse), that is, to use existing core assets such as architecture, requirements, testing, documentation to manufacture specific application products. In a 2008 report, researchers at Carnegie Mellon University’s Software Engineering Institute (CMU-SEI) claimed that software product lines can deliver the following benefits:

The software product line paints a rosy picture: product-level reuse with more than 90% reusability, agile customization on demand, domain architecture that ignores the impact of technological change, excellent and considerable economic benefits, and so on. The only problem with it is how to do it? Although software product line engineering attempts to strategically reuse all technical assets (including documentation, code, specifications, tools, etc.) At the organizational level by comprehensively utilizing all management and technical means, it still faces many difficulties in developing successful software product lines under the current mainstream technology system.

The concept of reversible computing is highly consistent with the theory of software product line, and its technical solution brings a new solution to the core technical difficulty of software product line-variability management. In software product line engineering, traditional variability management mainly includes three approaches: adaptation, replacement, and extension, 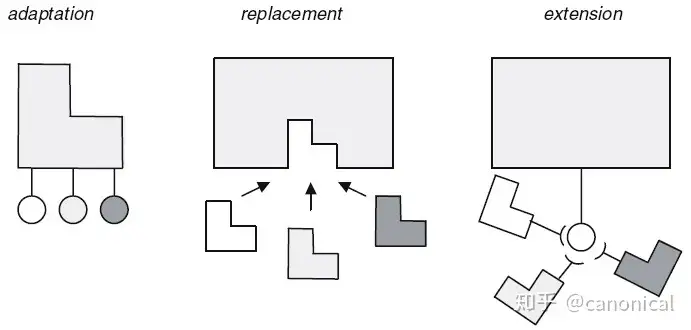all of which can be seen as adding functionality to the core architecture. But the barrier to reusability comes not only from the inability to add new features, but also from the inability to shield existing features in many cases. Traditional adaptation technology requires consistent matching of interfaces, which is a rigid docking requirement. Once mismatched, it will lead to continuous upward conduction of stress, and ultimately the problem can only be solved by replacing components as a whole. Reversible computing complements the key mechanism of “elimination” for variability management through variance merging, and can construct flexible adaptation interfaces in the domain model space on demand, so as to effectively control the influence range of change points. Although the difference in reversible computation can also be interpreted as an extension of the basic model, there are obvious differences between it and plug-in extension technology. In the platform-plug-in structure, the platform is the core subject, and the plug-in is attached to the platform, more like a patch mechanism, which is a relatively minor part at the conceptual level. In the reversible calculation, through some formal transformations, we can get a formula with higher symmetry:

\[A = B \oplus G(D) \equiv (B,D)\]

If we regard G as a relatively invariant background knowledge, we can formally hide it and define a more advanced “bracket” operator, which is similar to the “inner product” in mathematics. In this form, B and D are dual, B is complementary to D, and D is complementary to B. At the same time, we notice that G (D) is the embodiment of model-driven architecture. The reason why model-driven is valuable is that small changes in model D can be amplified by G into a large number of derivative changes in the system. Therefore, G (D) is a nonlinear transformation, and B is the remaining part of the system after removing the nonlinear factors corresponding to D. When all the complex nonlinear factors are stripped out, the last remaining part B may be simple and even form a new domain model structure that can be understood independently (we can compare the relationship between sound waves and air, sound waves are disturbances of air, but we can directly use sine wave model to describe sound waves without studying the air itself). The form of A = (B, D) can be straightforwardly generalized to the case where more domain models exist

\[A = (B,D,E,F,...)\]

Because concepts such as B, D, and E are all domain models described by a certain DSL, they can be interpreted as the components generated by the projection of A to a specific domain model subspace, that is, the application A can be represented as a “Feature Vector,” for example

\[App = (Workflow, Report, Auth, ...)\]

Compared with Feature Oriented Programming (FOP), which is commonly used in software product lines, the feature decomposition scheme of reversible computing emphasizes the domain-specific description, the feature boundaries are more explicit, and the conceptual conflicts arising from feature synthesis are easier to deal with. The feature vector itself constitutes a higher dimensional domain model, which can be further decomposed to form a model level column, such as definition.

\[D' \equiv (B,D) \\G'(D') \equiv B \oplus G(D)\]

, and suppose that D ′ can continue to decompose

\[D' = V\oplus M(U) = M'(U')\]

, then we can get

\[\begin{aligned} A &= B \oplus G(D)\\ &= G'(D')\\ &= G'(M'(U'))\\ &= G'M'(V,U) \end{aligned}\]

Finally, we can describe D ‘by the domain feature vector U’, and then describe the original model A by the domain feature vector D ‘. This construction strategy of reversible computing is similar to deep neural network, which is no longer limited to a single model with many adjustable parameters, but to build a series of models with different levels of abstraction and complexity, and to construct the final application through step-by-step refinement. From the perspective of reversible computing, the work of application engineering becomes the description of software requirements using feature vectors, and domain engineering is responsible for generating the final software according to the description of feature vectors.

Three. The incipient differential revolution

(I) Docker

Docker is an application container engine open sourced by startup dotCloud in 2013. It can package any application and its dependent environment into a lightweight, portable and self-contained Container, and create a new form of software development, deployment and delivery based on the container as a standardized unit. As soon as Docker was born, it killed Google’s own son lmctfy (Let Me Contain That For You) container technology, and also made Google’s other own son Go language become an Internet celebrity. After that, the development of Docker was out of control. In 2014, a Docker storm swept across the world, promoting the change of operating system kernel with unprecedented strength, instantly detonating the container cloud market under the momentum of many giants, and fundamentally changing the technical form of enterprise application from development, construction to deployment and operation of the whole life cycle.

The success of Docker technology stems from its essential reduction of software runtime complexity, and its technical solution can be seen as a special case of reversible computing theory. Docker’s core technology model can be summarized in the following formula

\[App = Docker\langle DockerFile \rangle \ unionfs\ BaseImage\]

Dockerfile is a domain-specific language for building container images, such as

FROM ubuntu:16.04
RUN useradd --user-group --create-home --shell /bin/bash work
RUN apt-get update -y && apt-get install -y python3-dev
COPY . /app
RUN make /app

ENV PYTHONPATH /FrameworkBenchmarks
CMD python /app/app.py

EXPOSE 8088

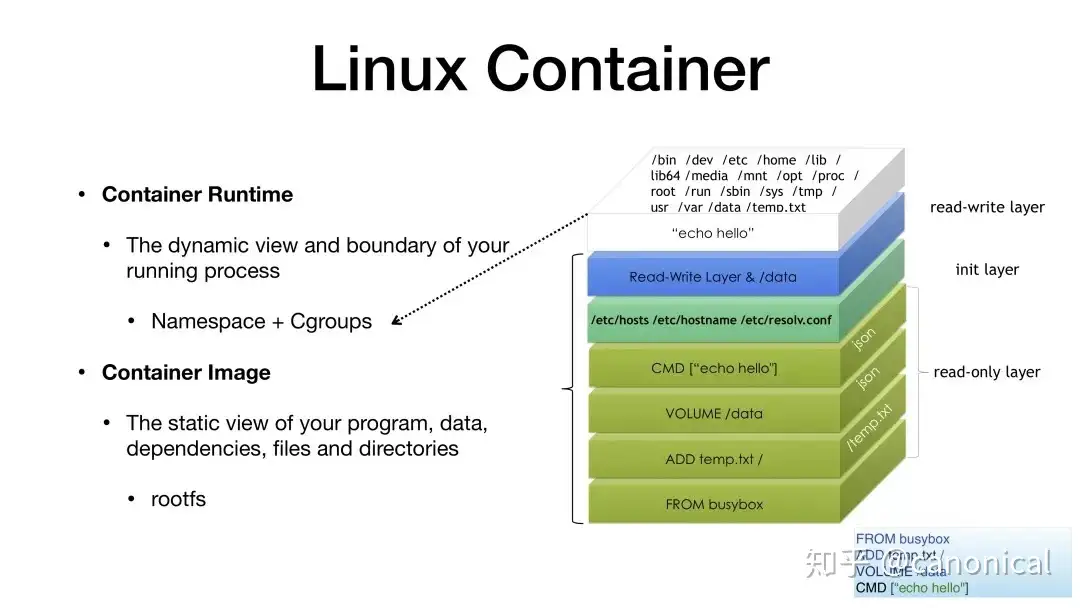
Dockerfile can be used to quickly and accurately describe the basic image, specific build steps, runtime environment variables, system configuration and other information on which the container depends. The Docker application plays the role of the Generator in reversible computing, interpreting the Dockerfile and executing the corresponding instructions to generate the container image. The creative use of the Union file system (Union FS) is a particular innovation of Docker. The file system is structured in layers, each of which is built and never changed, and any changes made on the latter layer are recorded only on its own layer. For example, when modifying a file in the previous layer, a copy is copied to the current layer by Copy-On-Write, while deleting the file in the previous layer does not actually delete the file, but only marks the file deleted in the current layer. Docker uses the federated file system to synthesize multiple container images into a complete application, and the essence of this technology is the AOP _ extends operation in reversible computing. Docker means stevedore in English, and the containers it handles are often compared to containers: standard containers are similar to containers, allowing us to transport/combine them freely without considering the specific contents of the container. But such comparisons are superficial and even misleading. The container is static, simple, and has no external interface, while the container is dynamic, complex, and has a lot of information interaction with the outside. This dynamic complex structure is as difficult to encapsulate into a so-called standard container as an ordinary static object. Without the introduction of a file system that supports variance, it is impossible to construct a flexible boundary to achieve logical separation. Docker’s standard encapsulation can also be done by virtual machines, and even the differential storage mechanism has been used to achieve incremental backup in virtual machines. What is the essential difference between Docker and virtual machines? Reviewing the three basic requirements of reversible computation for variance in the first section, we can clearly find the unique features of Docker.

(II) React

In 2013, the same year Docker was released, Facebook open-sourced React, a revolutionary Web front-end framework. The technical idea of React is very unique, which is based on the idea of functional programming, combined with a seemingly fantastic concept of Virtual DOM (Virtual DOM), introduced a set of new design patterns, and opened a new era of navigation for front-end development.

class HelloMessage extends React.Component {
  constructor(props) {
    super(props);
    this.state = { count: 0 };
    this.action = this.action.bind(this);
  }

  action(){
    this.setState(state => ({
      count: state.count + 1
    }));
  },

  render() {
    return (
      <button onClick={this.action}>
        Hello {this.props.name}:{this.state.count}
      </button>
    );
  }
}

ReactDOM.render(
  <HelloMessage name="Taylor" />,
  mountNode
);

The core of the React component is the Render function, which is designed with reference to the common template rendering technology in the backend. The main difference is that the backend template outputs HTML text, while the Render function of the React component uses JSX syntax similar to XML templates, and outputs virtual DOM node objects at runtime through compilation and transformation. For example, the render function of the HelloMessage component above is translated to a result similar to

render(){
   return new VNode("button", {onClick: this.action, 
          content: "Hello "+ this.props.name + ":" + this.state.count });
}

A React component can be described by the following formula:

\[VDom = render(state)\]

When the state changes, a new virtual DOM node is generated by re-executing the render function, and the virtual DOM node can be translated into a real HTML DOM object to update the interface. This rendering strategy of regenerating the full view based on state greatly simplifies front-end interface development. For example, for a list interface, traditional programming needs to write multiple different DOM operation functions such as new row/update row/delete row, while in React, you only need to change the state and re-execute the unique render function. The only problem with regenerating the dom view each time is that performance is poor, especially when there are many front-end interactions and state changes. React’s masterstroke is to propose a diff algorithm based on virtual DOM, which can automatically calculate the difference between two virtual DOM trees. When the state changes, it only needs to execute the DOM modification operation corresponding to the difference of virtual Dom (when updating the real DOM, it will trigger style calculation and layout calculation, resulting in low performance. While manipulating the virtual DOM in JavaScript is very fast). The overall strategy can be expressed as the following formula

\[state = state_0 \oplus state_1\\ \Delta VDom = render(state_1) - render(state_0)\\ \Delta Dom = Translator(\Delta VDom)\]

Obviously, this strategy is also a special case of reversible computation. If you pay a little attention, you will find that in recent years, more and more concepts such as merge/diff/residual/delta have appeared in the field of software design. For example, in the stream computing engine in the field of big data, the relationship between streams and tables can be expressed as

The operations of adding, deleting, modifying, and querying a table can be encoded as a stream of events, and the events representing data changes are accumulated together to form a data table. Modern science originated from the invention of calculus, and the essence of differential is the automatic calculation of infinitesimal difference, while integral is the inverse operation of differential, which automatically collects and merges infinitesimal quantities. In the 1870s, economics experienced a marginal revolution, which introduced the idea of calculus into economic analysis and rebuilt the whole economic edifice on the basis of the concept of margin. Today, the development of software construction theory has entered a bottleneck, and it is time to re-recognize the difference.

Four. Conclusion

The author’s professional background is theoretical physics. Reversible computation originated from the author’s attempt to introduce the ideas of physics and mathematics into the field of software. It was first proposed by the author around 2007. For a long time, the application of natural laws in the field of software is generally limited to the category of “simulation”, such as fluid dynamics simulation software, which contains some of the most profound world laws recognized by human beings, but these laws have not been used to guide and define the structure and evolution of the software world itself. Not the software world itself. In my opinion, in the software world, we can stand in the “God’s perspective”, plan and define a series of structural rules, and assist us to complete the construction of the software world. In order to do this, we first need to establish the “calculus” in the program world.

Similar to calculus, the core of reversible computation theory is to promote “difference quantity” to the concept of primacy, and to regard total quantity as a special case of difference quantity (total quantity = identity element + total quantity). In the traditional program world, what we express is only “have”, and it is “all”, the difference can only be obtained indirectly through the operation between the whole quantity, its expression and manipulation need special treatment, but based on the reversible computing theory, we should first define the expression form of all the difference concepts, and then establish the whole domain concept system around these concepts. In order to ensure the completeness of the mathematical space in which the difference is located (the result of the operation between the difference still needs to be a legal difference), the expression of the difference can not only be “existence”, but also a mixture of “existence” and “non-existence”. That is, the differential must be “reversible.”. Reversibility has a very deep physical connotation, and many very difficult software construction problems can be solved by embedding this concept in the basic concept system. In order to deal with distributed problems, modern software development systems have accepted the concept of immutable data, and in order to solve the problem of large-grained software reuse, we also need to accept the concept of immutable logic (reuse can be seen as keeping the original logic unchanged, and then adding variance descriptions). At present, there have been some creative practices of active application of the concept of difference in the industry, which can be interpreted uniformly under the theoretical framework of reversible computing. In this paper, a new programming language, X language, is presented, which can greatly simplify the technical implementation of reversible computation. At present, the author has designed and implemented a series of software frameworks and production tools based on X language, and proposed a new software production paradigm (NOP) based on them.

NopPlatform, a low-code platform based on reversible computing theory, has been open sourced: